Autor:
Mark Sanchez
Data E Krijimit:
28 Janar 2021
Datën E Azhurnimit:
1 Korrik 2024
Përmbajtje
Funksioni racional ka formën y = N (x) / D (x), ku N dhe D janë polinome. Për të përcaktuar me saktësi një funksion të tillë, keni nevojë për një njohuri të mirë të algjebrës, përfshirë llogaritjet diferenciale. Konsideroni shembullin e mëposhtëm: y = (2x - 6x + 5)/(4x + 2).
Hapa
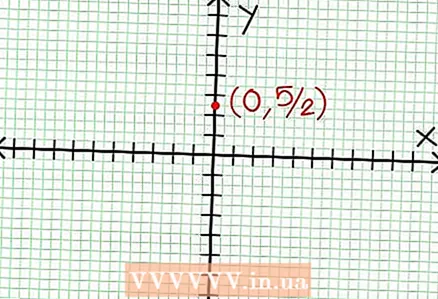1 Gjeni ndërprerjen y të grafikut. Për ta bërë këtë, zëvendësoni x = 0 në funksion dhe merrni y = 5/2. Kështu, pika e kryqëzimit të grafikut me boshtin Y ka koordinata (0, 5/2).Vendoseni këtë pikë në planin koordinativ. 
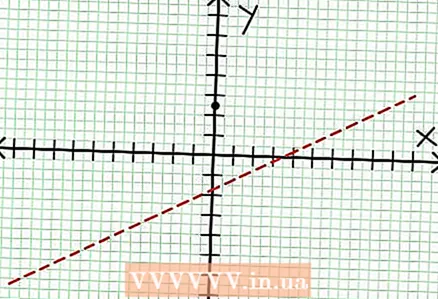2 Gjeni asimptotat horizontale. Ndani numëruesin me emëruesin (në një kolonë) për të përcaktuar sjelljen e "y" me vlerat e "x" që priren në pafundësi. Në shembullin tonë, ndarja do të jetë y = (1/2)x - (7/4) + 17/(8x + 4). Për vlera të mëdha pozitive ose negative të "x" 17 / (8x + 4) tenton në zero, dhe grafiku i afrohet vijës së drejtë të dhënë nga funksioni y = (1/2)x - (7/4). Duke përdorur vijën me pika, vizatoni këtë funksion. - Nëse shkalla e numëruesit është më e vogël se shkalla e emëruesit, atëherë nuk mund ta ndani numëruesin me emëruesin dhe asimptota do të përshkruhet nga funksioni në = 0.
- Nëse shkalla e numëruesit është e barabartë me shkallën e emëruesit, atëherë asimptota është një vijë horizontale e barabartë me raportin e koeficientëve në "x" në shkallën më të lartë.
- Nëse shkalla e numëruesit është 1 më shumë se shkalla e emëruesit, atëherë asimptota është një vijë e drejtë e prirur, pjerrësia e së cilës është e barabartë me raportin e koeficientëve në "x" në shkallën më të lartë.
- Nëse shkalla e numëruesit është më e madhe se shkalla e emëruesit me 2, 3, etj., Atëherë për vlera të mëdha |NS| kuptim në priren drejt pafundësisë (pozitive ose negative) në formën e një shkalle katrore, kub ose shkallë tjetër të një polinomi. Në këtë rast, ka shumë të ngjarë, nuk keni nevojë të ndërtoni një grafik të saktë të funksionit të marrë duke e ndarë numëruesin me emëruesin.
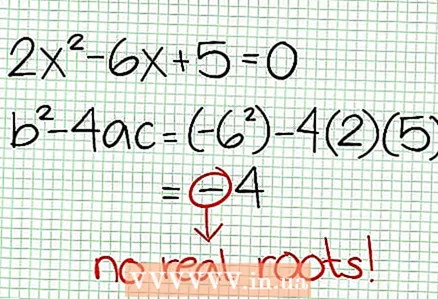3 Gjeni zero të funksionit. Një funksion racional ka zero kur numëruesi i tij është zero, domethënë N (NS) = 0. Në shembullin tonë, 2x - 6x + 5 = 0. Diskriminuesi i këtij ekuacioni katror: b - 4ac = 6 - 4 * 2 * 5 = 36 - 40 = -4. Meqenëse diskriminuesi është negativ, atëherë N (NS), dhe kështu F (NS) nuk ka rrënjë të vërteta. Grafiku i një funksioni racional nuk kryqëzon boshtin X. Nëse funksioni ka zero (rrënjë), atëherë vendosini ato në planin koordinativ. 
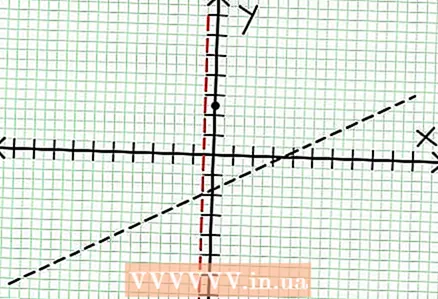4 Gjeni asimptotat vertikale. Për ta bërë këtë, vendosni emëruesin në zero. Në shembullin tonë, 4x + 2 = 0 dhe NS = -1/2. Hartoni asimptotën vertikale duke përdorur vijën me pika. Nëse për ndonjë vlerë NS N (NS) = 0 dhe D (NS) = 0, atëherë asimptota vertikale ose ekziston ose nuk ekziston (ky është një rast i rrallë, por është më mirë ta mbani mend). 
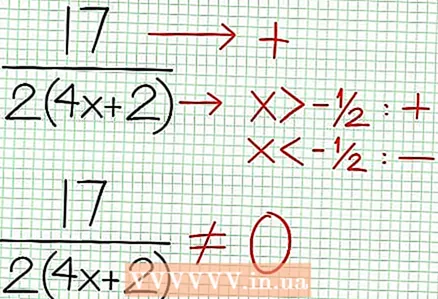5 Shikoni pjesën e mbetur të numëruesit të ndarë me emëruesin. A është pozitive, negative, apo zero? Në shembullin tonë, pjesa e mbetur është 17, e cila është pozitive. Emëruesi 4x + 2 pozitive në të djathtë të asimptotës vertikale dhe negative në të majtë të saj. Kjo do të thotë se grafiku i funksionit racional për vlera të mëdha pozitive NS i afrohet asimptotës nga lart, dhe për vlera të mëdha negative NS - nga poshtë. Që nga 17 / (8x + 4) nuk është kurrë e barabartë me zero, atëherë grafiku i këtij funksioni nuk do të ndërpresë kurrë vijën e drejtë të përcaktuar nga funksioni në = (1/2)NS - (7/4). 
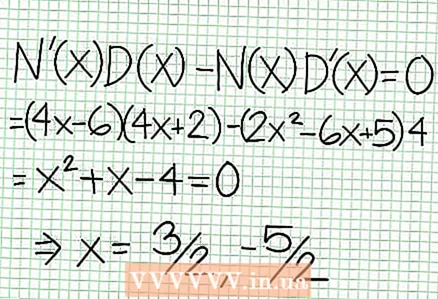6 Gjeni ekstrema lokale. Ekziston një ekstrem lokal për N '(x) D (x) - N (x) D ’(x) = 0. Në shembullin tonë, N ’(x) = 4x - 6 dhe D '(x) = 4. N ’(x) D (x) - N (x) D ’(x) = (4x - 6)(4x + 2) - (2x - 6x + 5)*4 = x + x - 4 = 0. Duke zgjidhur këtë ekuacion, ju gjeni atë x = 3/2 dhe x = -5/2. (Këto nuk janë vlera plotësisht të sakta, por ato janë të përshtatshme për rastin tonë kur nuk nevojitet super precizion.) 
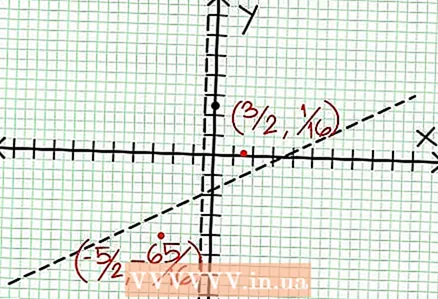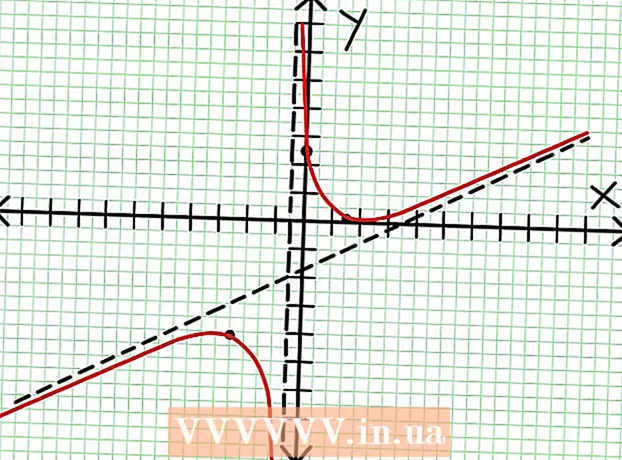
7 Gjeni vlerën në për çdo ekstrem lokal. Për ta bërë këtë, zëvendësoni vlerat NS në funksionin origjinal racional. Në shembullin tonë, f (3/2) = 1/16 dhe f (-5/2) = -65/16. Vendosni mënjanë pikat (3/2, 1/16) dhe (-5/2, -65/16) në planin koordinativ. Meqenëse llogaritjet bazohen në vlera të përafërta (nga hapi i mëparshëm), minimumi dhe maksimumi i gjetur gjithashtu nuk janë plotësisht të saktë (por ndoshta shumë afër vlerave të sakta). (Pika (3/2, 1/16) është shumë afër minimumit lokal. Duke filluar nga hapi 3, ne e dimë se në gjithmonë pozitive për NS> -1/2, dhe gjetëm një vlerë të vogël (1/16); kështu, vlera e gabimit është jashtëzakonisht e vogël në këtë rast.)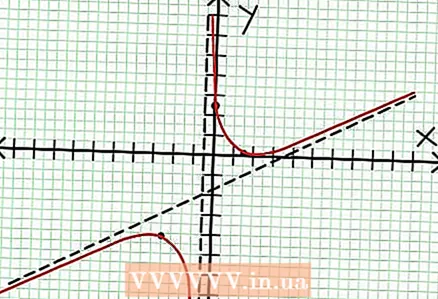 
8 Lidhni pikat në pritje dhe zgjasni pa probleme grafikun në asimptotat (mos harroni drejtimin e saktë të grafikut që i afrohet asimptotave). Mos harroni se grafiku nuk duhet të kalojë boshtin X (shiko hapin 3). Grafiku gjithashtu nuk ndërpritet me asimptotat horizontale dhe vertikale (shih hapin 5). Mos e ndryshoni drejtimin e tabelës përveç në pikat ekstreme të gjetura në hapin e mëparshëm.
Këshilla
- Nëse i keni ndjekur rreptësisht hapat e mësipërm, atëherë nuk ka nevojë të llogaritni derivatet e dytë (ose sasi të ngjashme komplekse) për të testuar zgjidhjen tuaj.
- Nëse nuk keni nevojë të llogaritni vlerat e sasive, mund të zëvendësoni gjetjen e ekstremave lokale duke llogaritur disa palë koordinata shtesë (NS, në) midis secilës palë asimptotash. Për më tepër, nëse nuk ju intereson se si funksionon metoda e përshkruar, atëherë mos u habitni pse nuk mund të gjeni derivatin dhe të zgjidhni ekuacionin N '(x) D (x) - N (x) D ’(x) = 0.
- Në disa raste, do të duhet të punoni me polinome të rendit më të lartë. Nëse nuk mund të gjeni zgjidhjen e saktë duke përdorur faktorizimin, formulat, etj., Atëherë vlerësoni zgjidhjet e mundshme duke përdorur metoda numerike siç është metoda e Njutonit.
- Në raste të rralla, numëruesi dhe emëruesi ndajnë një faktor të përbashkët të ndryshueshëm. Sipas hapave të përshkruar, kjo do të çojë në zero dhe një asimptotë vertikale në të njëjtin vend. Sidoqoftë, kjo nuk është e mundur, dhe shpjegimi është një nga sa vijon:
- Zero në N (NS) ka një shumëllojshmëri më të lartë se zero në D (NS) Grafiku F (NS) tenton të jetë zero në këtë pikë, por nuk përcaktohet atje. Tregojeni këtë duke vizatuar një rreth rreth pikës.
- Zero në N (NS) dhe zero në D (NS) kanë të njëjtën shumëllojshmëri. Grafiku i afrohet një pike jo-zero në këtë vlerë NSpor të papërcaktuara në të. Tregojeni këtë duke vizatuar një rreth rreth pikës.
- Zero në N (NS) ka një shumëllojshmëri më të ulët se zero në D (NS) Këtu ka një asimptotë vertikale.
