Si të zgjidhni një ekuacion linear Diofantin

Autor: Mark Sanchez
Data E Krijimit: 5 Janar 2021
Datën E Azhurnimit: 1 Korrik 2024
Anonim
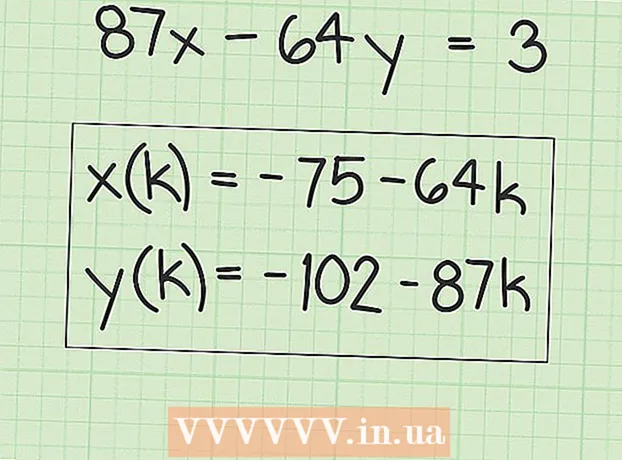
Si të zgjidhni një ekuacion linear Diofantin - Shoqëri
Si të zgjidhni një ekuacion linear Diofantin - Shoqëri

Përmbajtje

Për të zgjidhur një ekuacion linear Diofantin, duhet të gjeni vlerat e variablave "x" dhe "y", të cilët janë numra të plotë. Një zgjidhje e plotë është më komplekse se zakonisht dhe kërkon një grup të caktuar veprimesh. Së pari, duhet të llogaritni pjesëtuesin më të madh të përbashkët (GCD) të koeficientëve, dhe pastaj të gjeni një zgjidhje. Pasi të keni gjetur një zgjidhje të plotë për një ekuacion linear, mund të përdorni një model të thjeshtë për të gjetur një numër të pafund zgjidhjesh të tjera.

Hapa

Pjesa 1 nga 4: Si të shkruani një ekuacion

  1. 1 Shkruani ekuacionin në formë standarde. Një ekuacion linear është një ekuacion në të cilin eksponentët e variablave nuk i kalojnë 1. Për të zgjidhur një ekuacion të tillë linear, së pari shkruajeni atë në formë standarde. Forma standarde e një ekuacioni linear duket kështu: Ax+By=C{ displaystyle Ax + By = C}, ku A,B{ stili i ekranit A, B} dhe C{ displaystyle C} - numra të plotë.
    • Nëse ekuacioni jepet në një formë të ndryshme, silleni në formë standarde duke përdorur operacionet bazë algjebrike. Për shembull, duke pasur parasysh ekuacionin 23x+4y−7x=−3y+15{ displaystyle 23x + 4y -7x = -3y + 15}... Jepni terma të ngjashëm dhe shkruani ekuacionin si ky: 16x+7y=15{ displaystyle 16x + 7y = 15}.
  2. 2 Thjeshtoni ekuacionin (nëse është e mundur). Kur shkruani ekuacionin në formë standarde, shikoni koeficientët A,B{ stili i ekranit A, B} dhe C{ displaystyle C}... Nëse këto shanse kanë një GCD, ndani të tre shanset me të. Zgjidhja e një ekuacioni kaq të thjeshtuar do të jetë gjithashtu zgjidhja e ekuacionit origjinal.
    • Për shembull, nëse të tre koeficientët janë çift, ndajini ato me të paktën 2. Për shembull:
      • 42x+36y=48{ displaystyle 42x + 36y = 48} (të gjithë anëtarët ndahen me 2)
      • 21x+18y=24{ displaystyle 21x + 18y = 24} (tani të gjithë anëtarët ndahen me 3)
      • 7x+6y=8{ displaystyle 7x + 6y = 8} (ky ekuacion nuk mund të thjeshtohet më)
  3. 3 Kontrolloni nëse ekuacioni mund të zgjidhet. Në disa raste, mund të thuash menjëherë se ekuacioni nuk ka zgjidhje. Nëse koeficienti "C" nuk ndahet me GCD të koeficientëve "A" dhe "B", ekuacioni nuk ka zgjidhje.
    • Për shembull, nëse të dy koeficientët A{ stili i ekranit A} dhe B{ displaystyle B} janë çift, atëherë koeficienti C{ displaystyle C} duhet të jetë e barabartë. Por nëse C{ displaystyle C} e çuditshme, atëherë nuk ka zgjidhje.
      • Ekuacioni 2x+4y=21{ displaystyle 2x + 4y = 21} nuk ka zgjidhje të plota.
      • Ekuacioni 5x+10y=17{ displaystyle 5x + 10y = 17} nuk ka zgjidhje të plota pasi ana e majtë e ekuacionit ndahet me 5 dhe ana e djathtë jo.

Pjesa 2 nga 4: Si të shkruani algoritmin e Euklidit

  1. 1 Kuptoni algoritmin e Euklidit. Shtë një seri ndarjesh të përsëritura në të cilat pjesa e mëparshme përdoret si pjesëtues i radhës. Pjestuesi i fundit që ndan numrat në mënyrë integrale është pjesëtuesi më i madh i përbashkët (GCD) i dy numrave.
    • Për shembull, le të gjejmë GCD të numrave 272 dhe 36 duke përdorur algoritmin e Euklidit:
      • 272=7∗36+20{ displaystyle 272 = 7 * 36 + 20} - Ndani numrin më të madh (272) me atë më të vogël (36) dhe kushtojini vëmendje pjesës tjetër (20);
      • 36=1∗20+16{ displaystyle 36 = 1 * 20 + 16} - pjesëtoni pjestuesin e mëparshëm (36) me pjesën e mëparshme (20). Vini re mbetjen e re (16);
      • 20=1∗16+4{ displaystyle 20 = 1 * 16 + 4} - pjesëtoni pjestuesin e mëparshëm (20) me pjesën e mëparshme (16). Vini re mbetjen e re (4);
      • 16=4∗4+0{ displaystyle 16 = 4 * 4 + 0} - Ndani pjestuesin e mëparshëm (16) me pjesën e mëparshme (4). Meqenëse pjesa e mbetur është 0, mund të themi se 4 është GCD e dy numrave origjinal 272 dhe 36.
  2. 2 Aplikoni algoritmin e Euklidit në koeficientët "A" dhe "B". Kur shkruani ekuacionin linear në formë standarde, përcaktoni koeficientët "A" dhe "B" dhe më pas aplikoni algoritmin e Euklidit tek ata për të gjetur GCD. Për shembull, duke pasur parasysh një ekuacion linear 87x−64y=3{ displaystyle 87x-64y = 3}.
    • Këtu është algoritmi i Euklidit për koeficientët A = 87 dhe B = 64:
      • 87=1∗64+23{ displaystyle 87 = 1 * 64 + 23}
      • 64=2∗23+18{ displaystyle 64 = 2 * 23 + 18}
      • 23=1∗18+5{ displaystyle 23 = 1 * 18 + 5}
      • 18=3∗5+3{ displaystyle 18 = 3 * 5 + 3}
      • 5=1∗3+2{ displaystyle 5 = 1 * 3 + 2}
      • 3=1∗2+1{ displaystyle 3 = 1 * 2 + 1}
      • 2=2∗1+0{ displaystyle 2 = 2 * 1 + 0}
  3. 3 Gjeni faktorin më të madh të përbashkët (GCD). Meqenëse pjesëtuesi i fundit ishte 1, GCD 87 dhe 64 janë 1. Kështu, 87 dhe 64 janë numra të thjeshtë në lidhje me njëri -tjetrin.
  4. 4 Analizoni rezultatin. Kur gjeni koeficientët gcd A{ stili i ekranit A} dhe B{ displaystyle B}, krahasojeni atë me koeficientin C{ displaystyle C} ekuacioni origjinal. Nëse C{ displaystyle C} pjesëtohet me gcd A{ stili i ekranit A} dhe B{ displaystyle B}, ekuacioni ka një zgjidhje të plotë; përndryshe ekuacioni nuk ka zgjidhje.
    • Për shembull, ekuacioni 87x−64y=3{ displaystyle 87x-64y = 3} mund të zgjidhet sepse 3 pjesëtohet me 1 (gcd = 1).
    • Për shembull, supozoni GCD = 5. 3 nuk ndahet në mënyrë të barabartë me 5, kështu që ky ekuacion nuk ka zgjidhje të plota.
    • Siç tregohet më poshtë, nëse një ekuacion ka një zgjidhje të plotë, ai gjithashtu ka një numër të pafund zgjidhjesh të tjera të plota.

Pjesa 3 nga 4: Si të gjeni një zgjidhje duke përdorur algoritmin e Euklidit

  1. 1 Numëroni hapat për llogaritjen e GCD. Për të gjetur zgjidhjen për një ekuacion linear, duhet të përdorni algoritmin Euklidian si bazë për procesin e zëvendësimit dhe thjeshtimit.
    • Filloni duke numëruar hapat për llogaritjen e GCD. Procesi i llogaritjes duket si ky:
      • Hapi 1:87=(1∗64)+23{ displaystyle { text {Hapi 1}}: 87 = (1 * 64) +23}
      • Hapi 2:64=(2∗23)+18{ displaystyle { text {Hapi 2}}: 64 = (2 * 23) +18}
      • Hapi 3:23=(1∗18)+5{ displaystyle { text {Hapi 3}}: 23 = (1 * 18) +5}
      • Hapi 4:18=(3∗5)+3{ displaystyle { tekst {Hapi 4}}: 18 = (3 * 5) +3}
      • Hapi 5:5=(1∗3)+2{ displaystyle { tekst {Hapi 5}}: 5 = (1 * 3) +2}
      • Hapi 6:3=(1∗2)+1{ displaystyle { tekst {Hapi 6}}: 3 = (1 * 2) +1}
      • Hapi 7:2=(2∗1)+0{ displaystyle { text {Hapi 7}}: 2 = (2 * 1) +0}
  2. 2 Kushtojini vëmendje hapit të fundit, ku ka mbetur. Rishkruani ekuacionin për këtë hap për të izoluar pjesën e mbetur.
    • Në shembullin tonë, hapi i fundit me pjesën e mbetur është hapi 6. Pjesa e mbetur është 1. Rishkruani ekuacionin në hapin 6 si më poshtë:
      • 1=3−(1∗2){ displaystyle 1 = 3- (1 * 2)}
  3. 3 Izoloni pjesën e mbetur të hapit të mëparshëm. Ky proces është një "lëvizje lart" hap pas hapi. Çdo herë që do të izoloni pjesën e mbetur në ekuacion në hapin e mëparshëm.
    • Izoloni pjesën e mbetur të ekuacionit në Hapin 5:
      • 2=5−(1∗3){ displaystyle 2 = 5- (1 * 3)} ose 2=5−3{ displaystyle 2 = 5-3}
  4. 4 Zëvendësoni dhe thjeshtoni. Vini re se ekuacioni në hapin 6 përmban numrin 2, dhe në ekuacionin në hapin 5, numri 2 është i izoluar. Pra, në vend të "2" në ekuacionin në hapin 6, zëvendësoni shprehjen në hapin 5:
    • 1=3−2{ displaystyle 1 = 3-2} (ekuacioni i hapit 6)
    • 1=3−(5−3){ displaystyle 1 = 3- (5-3)} (në vend të 2, një shprehje u zëvendësua)
    • 1=3−5+3{ displaystyle 1 = 3-5 + 3} (kllapa të hapura)
    • 1=2(3)−5{ displaystyle 1 = 2 (3) -5} (e thjeshtuar)
  5. 5 Përsëriteni procesin e zëvendësimit dhe thjeshtimit. Përsëriteni procesin e përshkruar, duke lëvizur përmes algoritmit Euklidian në mënyrë të kundërt. Çdo herë që do të rishkruani ekuacionin nga hapi i mëparshëm dhe do ta lidhni atë në ekuacionin e fundit që merrni.
    • Hapi i fundit që shikuam ishte hapi 5. Pra, shkoni në hapin 4 dhe izoloni pjesën e mbetur në ekuacionin për atë hap:
      • 3=18−(3∗5){ displaystyle 3 = 18- (3 * 5)}
    • Zëvendësoni këtë shprehje me "3" në ekuacionin e fundit:
      • 1=2(18−3∗5)−5{ displaystyle 1 = 2 (18-3 * 5) -5}
      • 1=2(18)−6(5)−5{ displaystyle 1 = 2 (18) -6 (5) -5}
      • 1=2(18)−7(5){ displaystyle 1 = 2 (18) -7 (5)}
  6. 6 Vazhdoni me procesin e zëvendësimit dhe thjeshtimit. Ky proces do të përsëritet derisa të arrini hapin fillestar të algoritmit Euklidian. Qëllimi i procesit është të shkruajë ekuacionin me koeficientët 87 dhe 64 të ekuacionit origjinal që do të zgjidhet. Në shembullin tonë:
    • 1=2(18)−7(5){ displaystyle 1 = 2 (18) -7 (5)}
    • 1=2(18)−7(23−18){ displaystyle 1 = 2 (18) -7 (23-18)} (zëvendësoi shprehjen nga hapi 3)
      • 1=2(18)−7(23)+7(18){ displaystyle 1 = 2 (18) -7 (23) +7 (18)}
      • 1=9(18)−7(23){ displaystyle 1 = 9 (18) -7 (23)}
    • 1=9(64−2∗23)−7(23){ displaystyle 1 = 9 (64-2 * 23) -7 (23)} (zëvendësoi shprehjen nga hapi 2)
      • 1=9(64)−18(23)−7(23){ displaystyle 1 = 9 (64) -18 (23) -7 (23)}
      • 1=9(64)−25(23){ displaystyle 1 = 9 (64) -25 (23)}
    • 1=9(64)−25(87−64){ displaystyle 1 = 9 (64) -25 (87-64)} (zëvendësoi shprehjen nga hapi 1)
      • 1=9(64)−25(87)+25(64){ displaystyle 1 = 9 (64) -25 (87) +25 (64)}
      • 1=34(64)−25(87){ displaystyle 1 = 34 (64) -25 (87)}
  7. 7 Rishkruani ekuacionin që rezulton në përputhje me koeficientët origjinal. Kur të ktheheni në hapin e parë të algoritmit Euklidian, do të shihni se ekuacioni që rezulton përmban dy koeficientë të ekuacionit origjinal. Rishkruajeni ekuacionin në mënyrë që rendi i termave të tij të përputhet me koeficientët e ekuacionit origjinal.
    • Në shembullin tonë, ekuacioni origjinal 87x−64y=3{ displaystyle 87x-64y = 3}... Prandaj, rishkruani ekuacionin që rezulton në mënyrë që koeficientët të sillen në linjë.Kushtojini vëmendje të veçantë koeficientit "64". Në ekuacionin origjinal, ky koeficient është negativ, dhe në algoritmin Euklidian, ai është pozitiv. Prandaj, faktori 34 duhet të bëhet negativ. Ekuacioni përfundimtar do të shkruhet kështu:
      • 87(−25)−64(−34)=1{ displaystyle 87 (-25) -64 (-34) = 1}
  8. 8 Aplikoni shumëzuesin e duhur për të gjetur një zgjidhje. Vini re se në shembullin tonë, GCD = 1, pra ekuacioni përfundimtar është 1. Por ekuacioni origjinal (87x-64y) është 3. Prandaj, të gjitha termat në ekuacionin përfundimtar duhet të shumëzohen me 3 për të marrë zgjidhjen:
    • 87(−25∗3)−64(−34∗3)=1∗3{ displaystyle 87 (-25 * 3) -64 (-34 * 3) = 1 * 3}
    • 87(−75)−64(−102)=3{ displaystyle 87 (-75) -64 (-102) = 3}
  9. 9 Shkruani zgjidhjen e plotë të ekuacionit. Numrat që shumëzohen me koeficientët e ekuacionit origjinal janë zgjidhjet për atë ekuacion.
    • Në shembullin tonë, shkruani zgjidhjen si një palë koordinata: (x,y)=(−75,−102){ displaystyle (x, y) = ( - 75, -102)}.

Pjesa 4 nga 4: Gjeni zgjidhje të tjera të pafundme

  1. 1 Kuptoni që ka një numër të pafund zgjidhjesh. Nëse një ekuacion linear ka një zgjidhje të plotë, atëherë duhet të ketë pafundësisht shumë zgjidhje të plota. Këtu është një dëshmi e shpejtë (në formë algjebrike):
    • Ax+By=C{ displaystyle Ax + By = C}
    • A(x+B)+B(y−A)=C{ stili i ekranit A (x + B) + B (y-A) = C} (nëse shtoni "B" në "x" dhe zbritni "A" nga "y", vlera e ekuacionit origjinal nuk do të ndryshojë)
  2. 2 Regjistroni vlerat origjinale x dhe y. Modeli për llogaritjen e zgjidhjeve të ardhshme (të pafundme) fillon me zgjidhjen e vetme që keni gjetur tashmë.
    • Në shembullin tonë, zgjidhja është një palë koordinata (x,y)=(−75,−102){ displaystyle (x, y) = ( - 75, -102)}.
  3. 3 Shtoni faktorin "B" në vlerën "x". Bëni këtë për të gjetur vlerën e re x.
    • Në shembullin tonë, x = -75, dhe B = -64:
      • x=−75+(−64)=−139{ displaystyle x = -75 + ( - 64) = - 139}
    • Kështu, vlera e re "x": x = -139.
  4. 4 Zbrit faktorin "A" nga vlera "y". Kështu që vlera e ekuacionit origjinal të mos ndryshojë, kur shtoni një numër në "x", duhet të zbritni një numër tjetër nga "y".
    • Në shembullin tonë, y = -102, dhe A = 87:
      • y=−102−87=−189{ stili i ekranit y = -102-87 = -189}
    • Kështu, vlera e re për "y": y = -189.
    • Çifti i ri i koordinatave do të shkruhet kështu: (x,y)=(−139,−189){ displaystyle (x, y) = ( - 139, -189)}.
  5. 5 Kontrolloni zgjidhjen. Për të verifikuar që çifti i ri koordinativ është një zgjidhje për ekuacionin origjinal, futni vlerat në ekuacion.
    • 87x−64y=3{ displaystyle 87x-64y = 3}
    • 87(−139)−64(−189)=3{ displaystyle 87 (-139) -64 (-189) = 3}
    • 3=3{ displaystyle 3 = 3}
    • Meqenëse barazia është arritur, vendimi është i saktë.
  6. 6 Shkruani shprehjet për të gjetur shumë zgjidhje. Vlerat "x" do të jenë të barabarta me zgjidhjen origjinale plus çdo shumëfish të faktorit "B". Kjo mund të shkruhet si shprehja e mëposhtme:
    • x (k) = x + k (B), ku "x (k)" është grupi i vlerave "x" dhe "x" është vlera origjinale (e parë) e "x" që keni gjetur.
      • Në shembullin tonë:
      • x(k)=−75−64k{ stili i ekranit x (k) = - 75-64k}
    • y (k) = y-k (A), ku y (k) është grupi i vlerave y dhe y është vlera origjinale (e parë) y që keni gjetur.
      • Në shembullin tonë:
      • y(k)=−102−87k{ stili i ekranit y (k) = - 102-87k}

Duke Fituar Popullaritet

Si të shpëtoj nga një shtypje e një kolegu
Si të shpëtoj nga një shtypje e një kolegu
Parandaloni flokët e djegur në mot të lagësht
Parandaloni flokët e djegur në mot të lagësht
Shmangni pornografinë
Shmangni pornografinë
Bëni krem ​​për fytyrën
Bëni krem ​​për fytyrën